Understanding the shape:yl6axe4-ozq= pentagon: A Deep Dive into the Five-Sided Shape

Introduction

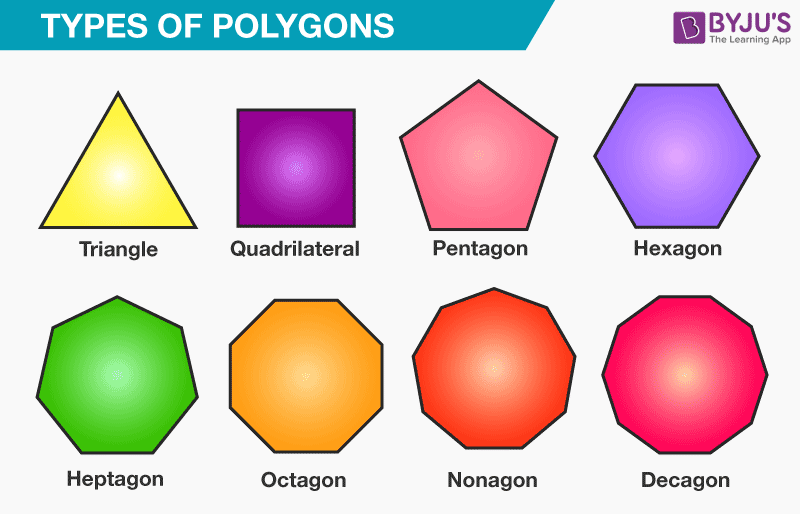
Geometry is an interesting field full of various shapes that are different from each other and have specific features and uses. Of these, the shape:yl6axe4-ozq= pentagon, which is a five sided polygon, has been seen aesthetically, and mathematically elegant in shape and has been found to have several uses in the modern world. For the lovers of math, or design or just plain geometric curiosity the pentagon is a great subject to explore.

What is a Pentagon?

The shape:yl6axe4-ozq= pentagon is a two dimensional shape whereby it consists of five straight lines and five interior angles. The word ‘pentagon’ is an adaptation of the Greecish words ‘penta’ meaning five and ‘gon’ meaning angle. This basic shape naturally attract’s mathematicians, artists and architects for centuries as it possesses symmetrical properties and various opportunities to create intricate patterns.

Types of Pentagons

However, this does not mean that each shape:yl6axe4-ozq= pentagon is the same. They can be classified based on their side lengths, angle measures, and overall shape:They can be classified based on their side lengths, angle measures, and overall shape:

Regular Pentagon

• All the five angles of the rectangle are equal.
• All interior angles of the larger pentagon are equal and each is equal to 108°.
• Exhibits perfect symmetry.

Irregular Pentagon

• Corners and measures of the sides are not equal.
• Asymmetrical compared to the just entire pentagons.

Convex Pentagon

• The sum of any two interior angles of a triangle is less than the sum of two right angles, that is 180 degrees.
• Sides extend outwards.

Concave Pentagon

• Interior angles of at least one pair of special polygons are equal to more than 180 degrees.
• One or more sides look like they are folding in.

Properties of a Pentagon

• Number of sides: 5
• Number of angles: 5
• Sum of interior angles: 5400 minutes
• Number of diagonals: 5
• Regular pentagon: They are all equal and therefore it is a square instead of a rectangle that has the sides; equal but perpendicular to each other.

The Pentagon in Nature and the World Around Us

Contrary to what you may think, the shape:yl6axe4-ozq= pentagon is much more present in our surroundings than one would expect. Here are some examples:

• Geometry: The shape:yl6axe4-ozq= pentagon is classified into basic figures which are used to develop complicated designs, forms and shapes.
• Nature: Flower petals of some plants, starfishes and some crystals possess five fold or pentagonal symmetry.
• Architecture: Buildings in the form of the Pentagon are present in the different cultures representing strength and stability.
• Design: Pentagon is incorporated in logos, manufactured items, and even designs needed for ornamentation.

Calculating Area and Perimeter of a Pentagon

They troubled themselves with the need to solve such mathematical problems as the pentagon area and shape:yl6axe4-ozq= pentagon perimeter in order to comprehend this geometrical figure deeply.

Perimeter

Perimeter is the total sum of all the sides of the pentagon. In order to find the perimeter, one has to add up the measure of all sides, that is five for this kind of polygon.

• Circuit = side 1 + side 2 + side 3 + side 4 + side 5

Area

Calculating the area of a regular shape:yl6axe4-ozq= pentagon involves using a specific formula:Calculating the area of a regular pentagon involves using a specific formula:

• Area = (1/4)√(5 + 2√5) side^2

Where:

• side = length of the one side of the shape:yl6axe4-ozq= pentagon

The Pentagon in Mathematics and Beyond

The pentagon holds a special place in mathematics due to its connections to other geometric concepts:The pentagon holds a special place in mathematics due to its connections to other geometric concepts:

• Golden Ratio: The regular pentagon is quite interconnected with the concept of the golden ratio, which is found in nature and art.
• Pythagorean Theorem: The next statement tells us that the pentagon can be divided into right triangles thus the Pythagorean theorem can be applied.
• Trigonometry: Miscellaneous real-life uses In trigonometry, properties of pentagons can be analyzed using trigonometric functions.

Applications of the Pentagon

The pentagon has a wide range of applications across various fields:The pentagon has a wide range of applications across various fields:

• Engineering: Applied in building of bridges, roofs and other construction.
• Architecture: Found in the building plans and the adornments of buildings and structures.
• Art and Design: Used as the basis for patterns, logos and other pieces of artwork.
• Military: The takes its name from its distinctive shape – it houses the U. S. Department of Defense.

FAQs

• What is a regular pentagon?

A regular pentagon is one where all the sides are of the same measure and all angles are of the same degree.

• What is a formula for finding the area of a pentagon?

There exists formula for the area of a pentagon; Area= (1/4) √(5 + 2√5) * side^2.

• What are examples of pentagons that are used in daily life?

These are for instance starfish, some crystals and buildings, especially the Pentagon.

• To begin with, it is possible to speak about a concave pentagon, but this kind of pentagon has more than five.

Yes, it is possible to have a concave pentagon if one or more of the interior angles are measured more than 180-degrees.

• The sum of the interior angles of a pentagon depends on the number of sides it has, which is 5; therefore, the sum of the interior angles of a pentagon is:.

Another possible interior angle is 108 degrees; another is 72 degrees The sum of the interior angles of a pentagon is 540 degrees.

Conclusion

The pentagon, which is not only the form of geometrical figure but also the form of the building of the supreme power, has been fascinating human brains for centuries. Regardless of its mathematical characteristics, uses, and cultural associations, this five-sided figure still captures people’s imagination. After the explanations of the individual types of pentagons, their characteristics, and the related computations. The audience will be able to grasp the workings and appeal behind this basic geometric shape. From the beginning to the end, getting to know the system of the shape:yl6axe4-ozq= pentagon is quite a fruitful and educative endeavour for any student. Business person or anyone who would wish to expand his or her horizon in this world.